Orbit Propagation
Orbit propagation can be an immensely complicated topic, spanning from two-body Keplerian motion, to models of gravitational fields including thousands of terms. Being able to pick the correct amount of precision required is difficult, and kete makes a number of judicious choices which are reasonable for the vast majority of cases.
What follows is a discussion of the pros-cons of various models of gravitational forces, and when the model is “good enough” for the problem at hand.
If we wish to predict the on-sky position or motion of an object, the level of precision required depends greatly upon the distance which the object is from the observer. Being accurate to 100nm when we are looking 5 au away is not necessary, alternatively, when we are considering an NEO such as Apophis (which will come very close to hitting the Earth), meters matter.
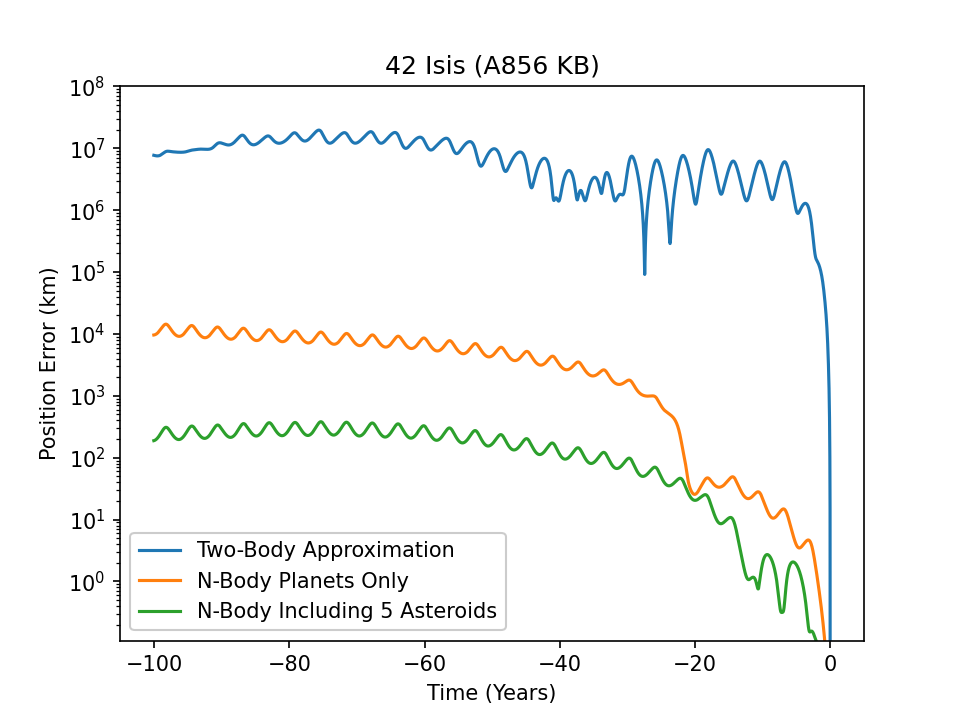
This is a plot of an arbitrary, rather large Main Belt Asteroid, and its orbital propagation error going back 100 years. Specifically error in orbit propagation comparing internal propagation against JPL Horizons SPICE kernels. This compares the difference in position for the two-body approximation, orbit propagation assuming there are no massive asteroids in the main belt, and finally including the 5 most massive main belt asteroids. Note that JPL Horizons includes at least 16 of the largest asteroids, so there is still residual error over the course of 100 years. This error however is only on the order of 100km.
Forces
First it is useful to list out forces which objects in space may experience, to get an understanding of what is required in order to accurately model their motion. These are listed in approximately the order of their effects on objects (though order may change due to varying circumstances).
Newtonian Gravity - Typically what is imagined when people say the force of gravity.
Corrections for Relativity (GR) - The orbit of Mercury precesses due to effects from relativity, and in fact many NEOs, or even objects which get close enough to planets will experience effects from relativity.
Gravity from Minor Planets - Main belt asteroids are often non-negligible. The motion of objects through the main belt often needs to include the mass of asteroids such as Ceres, which makes up an appreciable fraction of the total mass of the belt.
Oblateness of the Sun/Planets - The Sun and Planets are not ideal spheres, and as a result, cannot be exactly modeled as a point source. This non-sphericity can be written as an expansion of spherical harmonic-like terms, commonly written as J terms. The first non-trivial term of this expansion is the oblateness, referred to as J2. This term by itself will cause objects in orbit of the central mass to have their longitude of ascending node precess as a function of how inclined they are with respect to the equator of the central mass.
Non-gravitational Forces - The forces above are a result of gravity, however there are many potential forces which an object may experience, these include things such as outgassing, radiation pressure, the Yarkovsky effect, and the Poynting-Robertson effect. These effects typically have some relation to the total solar radiation that the object is receiving, and can frequently be written as a polynomial with respect to the distance that the object is from the Sun.
Accuracy
Accuracy of the orbit propagation depends on how precisely the forces above are computed, and the precision of the numerical integrator used. Forces such as the Yarkovsky effect cause relatively small forces on asteroids, but will add up to be non-negligible over the course of kilo-year or mega-years. A common issue however is that we often don’t have accurate enough measurements of the objects to be able to accurately measure the contribution of these forces.
Close encounters with other objects also cause significant accuracy issues as well. The force between objects follows a 1/r^2 relationship, meaning as the distance goes to zero, small changes in the distance cause large changes in the force. We do not have infinitely precise measurements of the objects orbits, meaning there is some positional error in our knowledge of every object. This error “blows up” during close encounters because of the small r effect. Many objects which cross the path of planets frequently will have relatively close encounters with planets with some regularity, making long term predictions of their orbits difficult. Typically it only takes a few close encounters to completely ruin any hope of predicting the position of an object in the future or past. This makes the inner solar system a chaotic system in the mathematical sense, small deviations of input parameters have large implications for future behavior (despite the fact that everything should in theory be precisely computable).
The result of the problems above, objects in the inner solar system of often very difficult to model more than a few hundred/thousand years into the future with any accuracy.
Performance
To achieve the highest accuracy, all forces listed above must be included. The downside for this is that it can be computationally expensive. If we wish to predict the position of minor planets for NEOWISE frames as an example, which are captured every 10-15 seconds, it would be wildly inefficient. Over the course of a few minutes objects motion can be modeled as linear, over hours (even days) the two-body approximation is often good enough. As a result of this, kete has tools for adaptively changing the approximation used in order to get good computational performance. The typical method is to use a full N-Body simulation to get the highest precision, then use that solution for the next day or so (adjustable) with two-body mechanics to query hundreds of times.
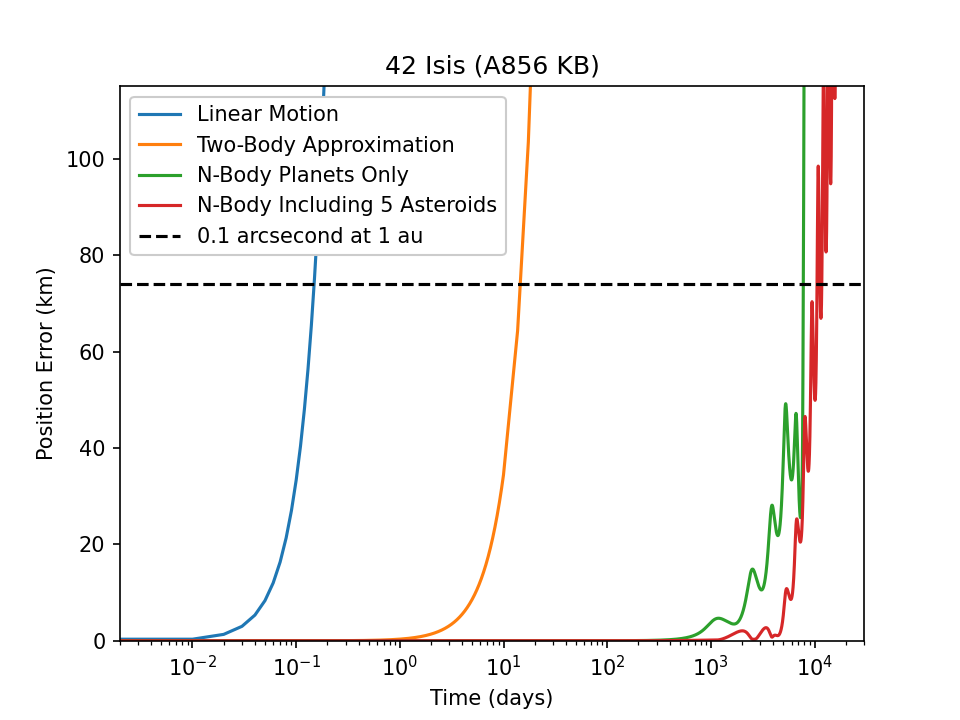
Demonstration of how quickly linear motion, two-body motion, and N-Body deviate from the true position. Linear motion is invalid within a few minutes, but two-body takes several days for this object to become significantly inaccurate. The dotted black line is how far an object must move tangentially to have an error of 0.1 arcseconds when it is 1 au from the observer (about 74km).