Note
Go to the end to download the full example code.
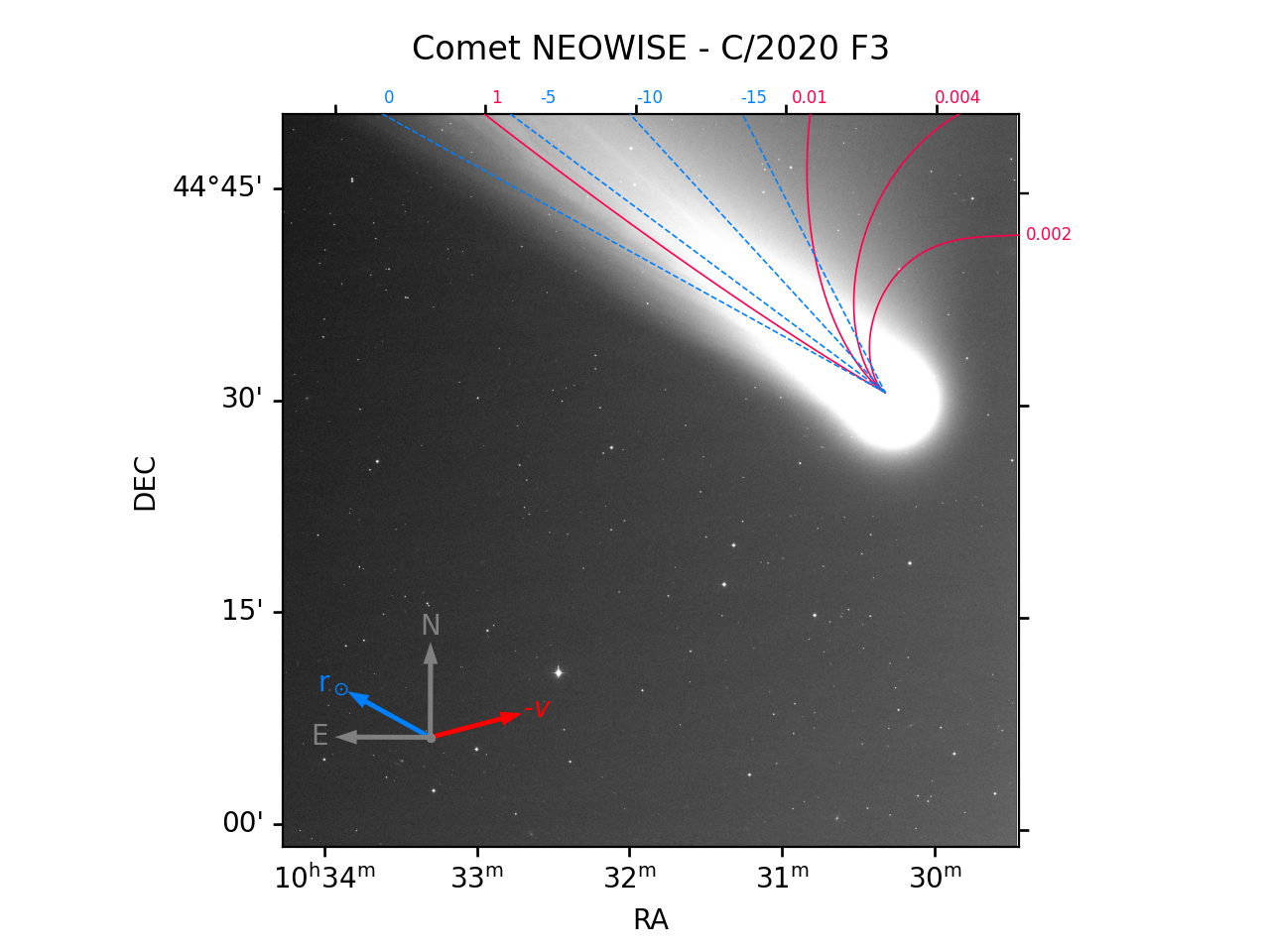
Annotated Comet
Given a specific FITs file containing a comet, annotate the plot with orbital information, such as diection of motion.
from astropy.wcs import WCS
import kete
import astropy
import numpy as np
import kete
import matplotlib.pyplot as plt
import numpy as np
# This is comet NEOWISE as observed by ZTF
state = kete.HorizonsProperties.fetch("C/2020 F3").state
# Specific frame information for the ZTF frame where neowise was imaged.
# See the tutorials for KONA and Precovery for more information on how to
# find all the times an object is observed.
frame_info = dict(
field=752,
filefracday=20200723164595,
ccdid=2,
filtercode="zg",
imgtypecode="o",
qid=3,
)
# Load the fits file for this ZTF frame.
frame = astropy.io.fits.open(kete.ztf.fetch_ZTF_file(**frame_info))[0]
# Grab frame information from this file
jd = kete.Time(frame.header["OBSJD"], scaling="utc").jd
frame_wcs = WCS(frame.header)
corners = []
dx, dy = frame_wcs.pixel_shape
for x, y in zip([dx, dx, 0, 0], [0, dy, dy, 0]):
coord = frame_wcs.pixel_to_world(x, y).icrs
corners.append(kete.Vector.from_ra_dec(coord.ra.deg, coord.dec.deg))
observer_loc = kete.spice.mpc_code_to_ecliptic("ZTF", jd)
# Build a kete FOV for this frame
fov = kete.ZtfCcdQuad(corners, observer_loc, maglimit=np.nan, fid=1, **frame_info)
# Compute the observation information for the comet in this frame
vis = kete.fov_state_check([state], [fov])[0]
def plot_vector(wcs, vec_a, vec_b, label, x=0.2, y=0.2, c="w", length=0.1, **kwargs):
"""
Given a world coordinate system, and 2 positions, plot a projected vector from
the vec_a toward vec_b in the given WCS. This is a fully generic plotting tool
which is used immediately below to plot the relavent vectors.
"""
vec_a = vec_a.as_equatorial
vec_b = vec_b.as_equatorial
pixels = wcs.world_to_pixel_values([vec_a.ra, vec_b.ra], [vec_a.dec, vec_b.dec])
diff_dir = np.diff(pixels, axis=1).ravel()
diff_dir /= np.linalg.norm(diff_dir)
shape = wcs.array_shape
length *= max(shape)
x *= shape[0]
y *= shape[1]
kwargs["lw"] = kwargs.get("lw", 0.01)
kwargs["width"] = kwargs.get("width", 20)
plt.arrow(x, y, *diff_dir * length, color=c, **kwargs)
plt.text(*(diff_dir * 1.5 * length + [x, y]), label, c=c, ha="center", va="center")
plt.scatter(x, y, c="grey", s=5)
def plot_vectors(wcs, state, fov, x=0.2, y=0.2):
"""
Plot 4 vectors using the WCS, the state of the object, and the FOV.
The vectors plotted are:
- Negative Velocity vector of the object, showing its motion.
- Position vector, showing the direction away from the sun.
- North vector, showing the Equatorial North.
- East vector, showing Equatorial East.
"""
past_vec = kete.propagate_n_body([state], state.jd - 0.05)[0].pos - fov.observer.pos
sun_vec = (state.pos * 1.001) - fov.observer.pos
vec = (state.pos - fov.observer.pos).as_equatorial
north_vec = kete.Vector.from_ra_dec(vec.ra, vec.dec + 0.01)
east_vec = kete.Vector.from_ra_dec(vec.ra + 0.01, vec.dec)
plot_vector(wcs, vec, past_vec, r"-$v$", x=x, y=y, c="r")
plot_vector(wcs, vec, sun_vec, r"r$_\odot$", x=x, y=y, c=(0, 0.5, 1))
plot_vector(wcs, vec, north_vec, r"N", c="grey", x=x, y=y, ls="--", lw=0.1)
plot_vector(wcs, vec, east_vec, r"E", c="grey", x=x, y=y, ls="--", lw=0.1)
def plot_syndyne(wcs, state, fov, beta, back_days=90, day_step=1, **kwargs):
"""
Plot a single syndyne line for the provided beta value.
"""
# create a non-grav model for the dust which will be used for propagation/
model = kete.propagation.NonGravModel.new_dust(beta)
# working backward, calculate the position of the comet at each time step
dust_state = kete.propagate_n_body([state], fov.jd - back_days)[0]
dust_states = []
for jd in np.arange(dust_state.jd, fov.jd, day_step):
dust_state = kete.propagate_n_body([dust_state], jd)[0]
dust_states.append(dust_state)
# Now treat all of those points as though they are release dust, and
# propagated to the current epoch.
cur_state = kete.propagate_n_body(
dust_states, fov.jd, non_gravs=[model] * len(dust_states)
)
# apply a light delay correction
cur_state = kete.propagate_two_body(cur_state, fov.jd, fov.observer.pos)
# Setup plotting
pos = [(x.pos - fov.observer.pos).as_equatorial for x in cur_state]
ras = [x.ra for x in pos]
decs = [x.dec for x in pos]
shape = wcs.array_shape
pix = []
for x, y in zip(*wcs.world_to_pixel_values(ras, decs)):
if not np.isfinite(x) or not np.isfinite(y):
continue
pix.append([x, y])
plt.xlim(0, shape[0])
plt.ylim(0, shape[1])
plt.plot(*np.transpose(pix), **kwargs)
def plot_synchrone(
wcs, state, fov, days_back, beta_max=1, beta_min=1e-5, beta_steps=100, **kwargs
):
"""
Plot a single sychrone line for the provided release day.
"""
# Sample beta values evenly in log space.
betas = np.logspace(np.log10(beta_min), np.log10(beta_max), beta_steps)[::-1]
# build non-grav models for each beta
models = [kete.propagation.NonGravModel.new_dust(beta) for beta in betas]
# propagate the comet back to the release date
dust_state = kete.propagate_n_body([state], fov.jd + days_back)[0]
dust_states = [dust_state] * len(betas)
# release dust and propagate foward to the current epoch.
cur_state = kete.propagate_n_body(dust_states, fov.jd, non_gravs=models)
# apply a light delay correction
cur_state = kete.propagate_two_body(cur_state, fov.jd, fov.observer.pos)
# setup plotting
pos = [(x.pos - fov.observer.pos).as_equatorial for x in cur_state]
ras = [x.ra for x in pos]
decs = [x.dec for x in pos]
shape = wcs.array_shape
pix = []
for x, y in zip(*wcs.world_to_pixel_values(ras, decs)):
if not np.isfinite(x) or not np.isfinite(y):
continue
pix.append([x, y])
plt.xlim(0, shape[0])
plt.ylim(0, shape[1])
plt.plot(*np.transpose(pix), **kwargs)
# Plot the final results
plt.figure(dpi=200)
frame = kete.ztf.fetch_frame(vis.fov)
wcs = kete.irsa.plot_fits_image(frame, percentiles=None)
plt.title("Comet NEOWISE - C/2020 F3\n")
# plot syndynes
for beta in [0.002, 0.004, 0.01, 0.04, 0.2]:
plot_syndyne(
wcs,
vis[0],
fov,
beta,
day_step=0.1,
lw=0.6,
c=(1, 0.0, 0.3),
label=f"{beta:0.2g}",
)
plot_syndyne(
wcs,
vis[0],
fov,
1,
back_days=10,
day_step=0.1,
lw=0.6,
c=(1, 0.0, 0.3),
label=f"{1:0.2g}",
)
# plot synchrones
for days in [-10, -15, -20, -25]:
plot_synchrone(
wcs, vis[0], fov, days, 0.1, ls="--", c=(0, 0.5, 1), lw=0.6, label=str(days)
)
plot_synchrone(wcs, vis[0], fov, -5, 0.8, ls="--", c=(0, 0.5, 1), lw=0.6, label=-5)
plot_synchrone(
wcs,
vis[0],
fov,
0.01,
1200000.0,
ls="--",
beta_steps=2000,
c=(0, 0.5, 1),
lw=0.6,
label=0,
)
# Fancy plotting of labels around the edge
shape = wcs.array_shape
xvals = []
for line in plt.gca().get_lines():
idx = np.argmax(
(line._y > 0)
& (line._y < wcs.array_shape[1])
& (line._x > 0)
& (line._x < wcs.array_shape[0])
)
edge = np.argmin(
[
abs(line._x[idx]),
abs(line._x[idx] - shape[0]),
abs(line._y[idx]),
abs(line._y[idx] - shape[1]),
]
)
offset = 30
if edge == 0:
label_pos = [0 - offset, line._y[idx]]
ha = "right"
va = "center"
elif edge == 1:
label_pos = [shape[0] + offset, line._y[idx]]
ha = "left"
va = "center"
elif edge == 2:
label_pos = [line._x[idx], 0 - offset]
ha = "center"
va = "bottom"
elif edge == 3:
label_pos = [line._x[idx], shape[0] + offset]
ha = "center"
va = "top"
plt.text(
*label_pos, line.get_label(), va=va, ha=ha, fontsize=6, color=line.get_color()
)
# add vectors
plot_vectors(frame_wcs, vis[0], vis.fov, y=0.85)
# for some reason astropy for this frame is plotting the y-axis inverted
# this just un-inverts it.
plt.gca().invert_yaxis()
plt.show()
Total running time of the script: (0 minutes 3.423 seconds)